Solvable Lie algebra
In mathematics, a Lie algebra g is solvable if its derived series terminates in the zero subalgebra. That is, writing
for the derived Lie algebra of g, generated by the set of values
- [x,y]
for x and y in g, the derived series
becomes constant eventually at 0.
Any nilpotent Lie algebra is solvable, a fortiori, but the converse is not true. The solvable Lie algebras and the semisimple Lie algebras form two large and generally complementary classes, as is shown by the Levi decomposition.
A maximal solvable subalgebra is called a Borel subalgebra. The largest solvable ideal is called the radical.
Contents |
Properties
Let  be a finite dimensional Lie algebra over a field of characteristic 0. The following are equivalent.
be a finite dimensional Lie algebra over a field of characteristic 0. The following are equivalent.
- (i)
 is solvable.
is solvable. - (ii)
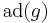 , the adjoint representation of
, the adjoint representation of  , is solvable.
, is solvable. - (iii) There is a finite sequence of ideals
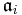 of
of  such that:
such that:
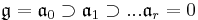 where
where ![[\mathfrak{a}_i, \mathfrak{a}_i] \subset \mathfrak{a}_{i%2B1}](/2012-wikipedia_en_all_nopic_01_2012/I/616941f86c645ff774401cf6eb9b0a5e.png) for all
for all  .
.
- (iv)
![[\mathfrak{g}, \mathfrak{g}]](/2012-wikipedia_en_all_nopic_01_2012/I/3f1683bcf0fa96e29329efca70a1d284.png) is nilpotent.
is nilpotent.
Lie's Theorem states that if  is a finite-dimensional vector space over an algebraically closed field of characteristic zero, and
is a finite-dimensional vector space over an algebraically closed field of characteristic zero, and  is a solvable linear Lie algebra over
is a solvable linear Lie algebra over  , then there exists a basis of
, then there exists a basis of  relative to which the matrices of all elements of
relative to which the matrices of all elements of  are upper triangular.
are upper triangular.
Example
- Every abelian Lie algebra is solvable.
- Every nilpotent Lie algebra is solvable.
- Every Lie subalgebra, quotient and extension of a solvable Lie algebra is solvable.
- Let
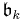 be a subalgebra of
be a subalgebra of 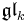 consisting of upper triangular matrices. Then
consisting of upper triangular matrices. Then 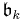 is solvable.
is solvable.
Solvable Lie groups
The terminology arises from the solvable groups of abstract group theory. There are several possible definitions of solvable Lie group. For a Lie group G, there is
- termination of the usual derived series, in other words taking G as an abstract group;
- termination of the closures of the derived series;
- having a solvable Lie algebra.
To have equivalence one needs to assume G connected. For connected Lie groups, these definitions are the same, and the derived series of Lie algebras are the Lie algebra of the derived series of (closed) subgroups.
See also
- Cartan's criterion
- Killing form
- Lie-Kolchin theorem
- Solvmanifold
- Dixmier mapping
External links
References
- Humphreys, James E. Introduction to Lie Algebras and Representation Theory. Graduate Texts in Mathematics, 9. Springer-Verlag, New York, 1972. ISBN 0-387-90053-5
![\mathfrak{g} \geq [\mathfrak{g},\mathfrak{g}] \geq [[\mathfrak{g},\mathfrak{g}],[\mathfrak{g},\mathfrak{g}]] \geq [[[\mathfrak{g},\mathfrak{g}],[\mathfrak{g},\mathfrak{g}]],[[\mathfrak{g},\mathfrak{g}],[\mathfrak{g},\mathfrak{g}]]] \geq ...](/2012-wikipedia_en_all_nopic_01_2012/I/6ed5d63e4eea5a29c8ad37304e44abc9.png)